一款操作系统
一款应用软件
一种通话设备
以上都不对
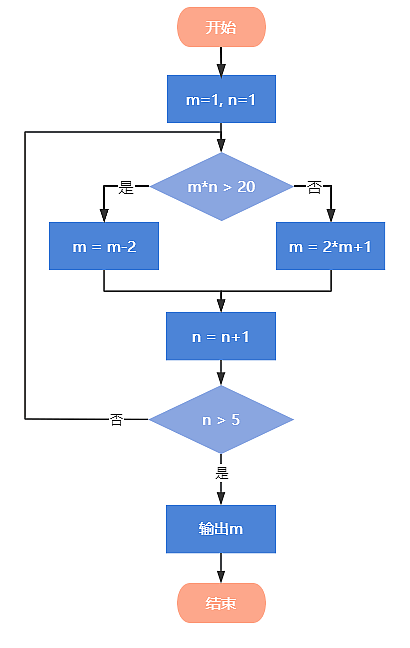
9
7
5
11
print() 函数的 sep 和 end 参数为带有默认值的命名关键字参数
print() 函数可以输出多个表达式的值，其参数为变长参数
如果 print() 函数同时使用 sep 和 end 参数，则要求 sep 在前 end 在后
print() 函数可以输出多个不同数据类型表达式的值
[1]
[1, 2, 4]
[1, 2, 4, 4]
触发异常
1, 2, 3
1, 2, 22
11, 11, 22
11, 11, 3
[1, 2, 3]
[1, 2, 3, 4]
[4]
None
(1, 2, 3),(1, 2, 3)
(1, 2, 3, 4),(1, 2, 3)
(1, 2, 3),(1, 2, 3, 4)
(1, 2, 3, 4),(1, 2, 3, 4)
[2, 3, 7, 11, 15]
[15, 11, 7, 3, 2]
[11, 2, 3, 7, 15]
None
O(n)
O(n2)
O(nlogn)
O(1)
dict99[(i, j)]
dict99[[i, j]]
dict99(i, j)
dict99{i, j}
[j for j in range(i) if i % j != 0]
[j for j in range(1,i 1) if i % j == 0]
[j for j in range(1,i 1) if i % j]
[j for j in range(i) if i % j == 0]
wb
w
rb
r
2#
1#4#
2#4#
2#3#4#
print(tuple(i**2 for i in range(10)))
print(tuple([i*i for i in range(1,10 1)]))
print(tuple(i*i for i in range(10 1)))
print(tuple(map(lambda x:x**2,range(10))))
lstA.remove(8)
lstA.pop(2)
del lstA[2]
lstA.del[2]
发表评论 取消回复