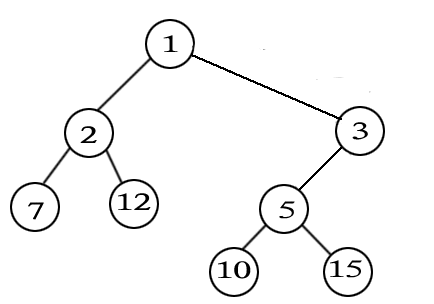
（笛卡尔树）对于一个给定的两两不等的正整数序列

（笛卡尔树）对于一个给定的两两不等的正整数序列，笛卡尔树是这样的一棵二叉树：首先，它是一个最小堆，即除了根结点，每个节点的权值都大雨父节点的权值；其次，它的中序遍历恰好就是给定的序列。例如，对于序列7、2、12、1、10、5、15、3，下图就是一棵对应的笛卡尔树。现输入序列的规模n（1≤n<100）和序列的 n 个元素，试求其对应的笛卡尔树的深度 d（根节点深度为1），以及有多少个叶子节点的深度为d。

#include

using namespace std;

const int SIZE=100 5;

const int INFINITY=1000000;

int n,a[SIZE],maxDeep,num;

void solve(int left,int right,int deep)

{

\tint i,j,min;

\tif(deep>maxDeep){

\t\tmaxDeep=deep;

\t\tnum=1;

\t}

\telse if(deep==maxDeep)

\t\t ① ;

\tmin= INFINITY;

\tfor(i=left;i<=right;i )

\t\tif(min>a[i]){

\t\t\tmin=a[i];

\t\t\t ② ;

\t\t}

\tif(left

\t ③ ;

\tif(j

\t ④ ;

}

int main()

{

\tint i;

\tcin>>n;

\tfor(i=1;i<=n;i )

\t\tcin>>a[i];

\tmaxDeep=0;

\tsolve(1,n,1);

\tcout<

\treturn 0;

}